Queues and Stacks
Abstract representation
In this chapter we will discuss a new container to store our data. The stacks and queues containers. Those also knows as Abstract data types, meaning we are defining the interface for the container not how it is actually implemented.
An abstract data Type (ADT) is defined by its behavior frm the point of view the user of the data, and by the operations it can accomplish with the data.
As a concrete example, the stack and queue have similar interfaces, but they are used for very different problems, as we shall see.
Queues
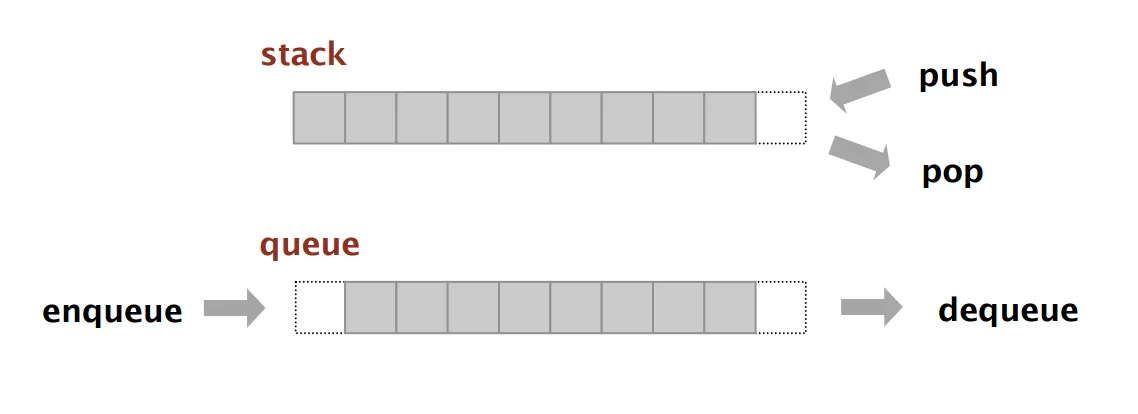
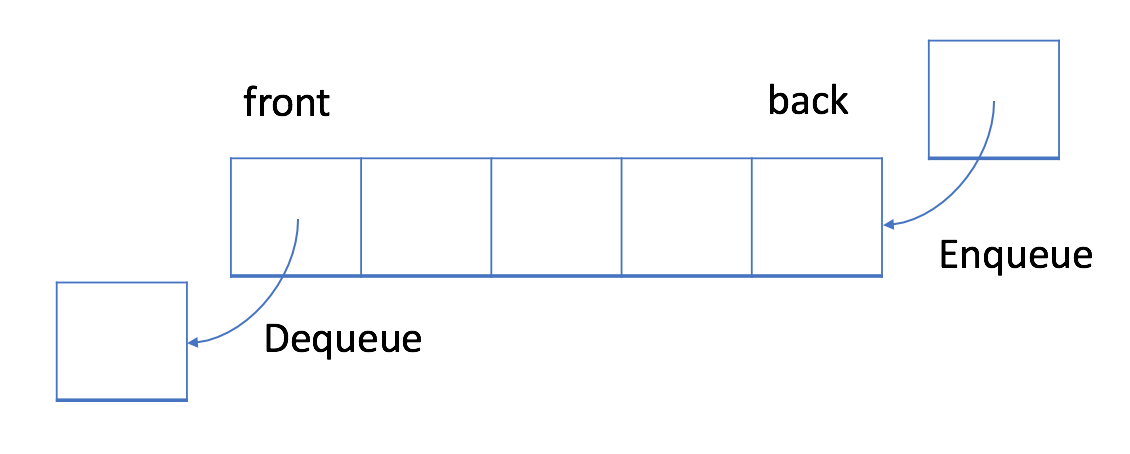
A queue or (First-in First Out) ADT is a collection where the first added element will be precessed first.
This ADT will have the following interface:
enqueue(value)place an entity onto the back of the queue.dequeue(): remove an entity from the front of the queue and return it.front(): look at the entity at the front of the queue, but don’t remove it.isEmpty()a boolean indicating the collection is empty or not.
Here is a example of the execution of this API.
Queue Q; // {} empty queue
Q.enqueue(42); // {42}
Q.enqueue(-3); // {42, -3}
Q.enqueue(17); // {42, -3, 17}
cout << Q.dequeue() << endl; // 42 ( Q is {-3, 17})
cout << Q.front() << endl; // -3 ( Q is {-3, 17})
cout << Q.dequeue() << endl; // -3 ( Q is {17})
Linked Lists implementation
For our first exercise, we will use linked list to represent the elements of the queue. You can
- Either use your proper imlementation of linked lists.
- Use the List class
Code in the demo
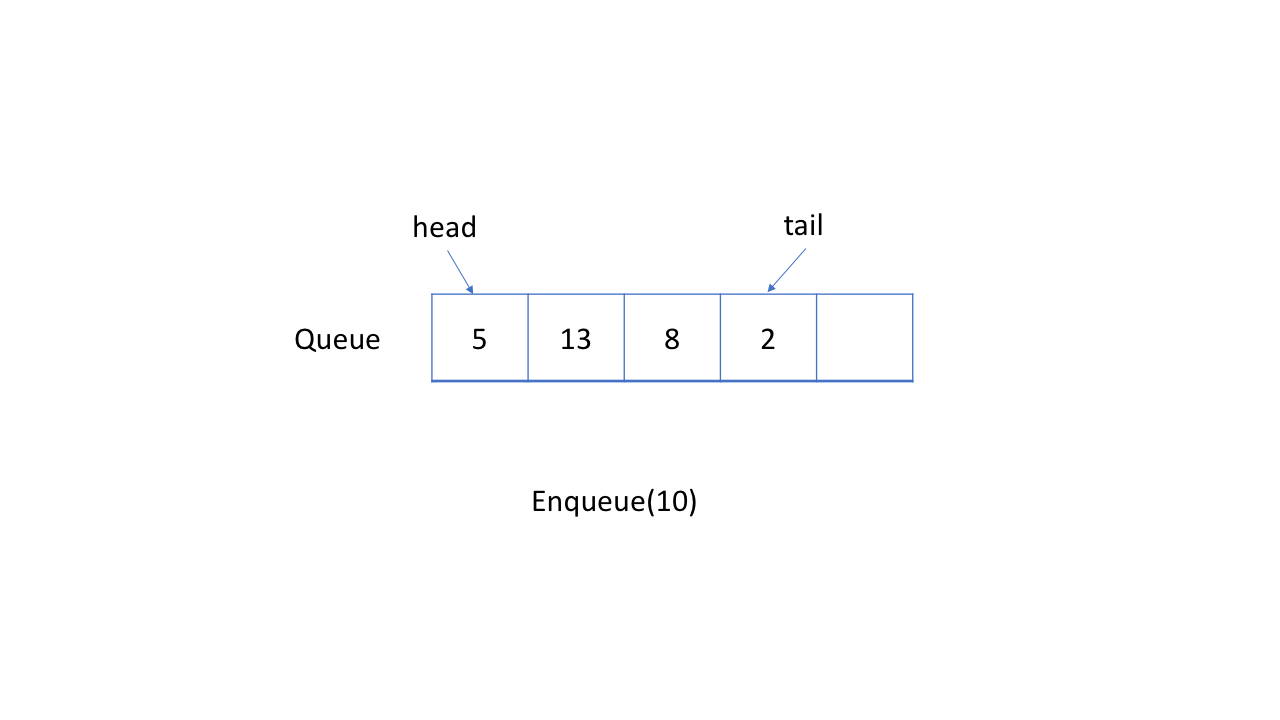
Circular array implementation
A more efficient way to implement a queue. Specially if we are limited by the use of a fixed size array is to use two pointers indicating the starting and the ending position.
The goad is to reuse the wasted storage freed by the dequeue operations.
Here is a link of the exercise on code step by step
Stack
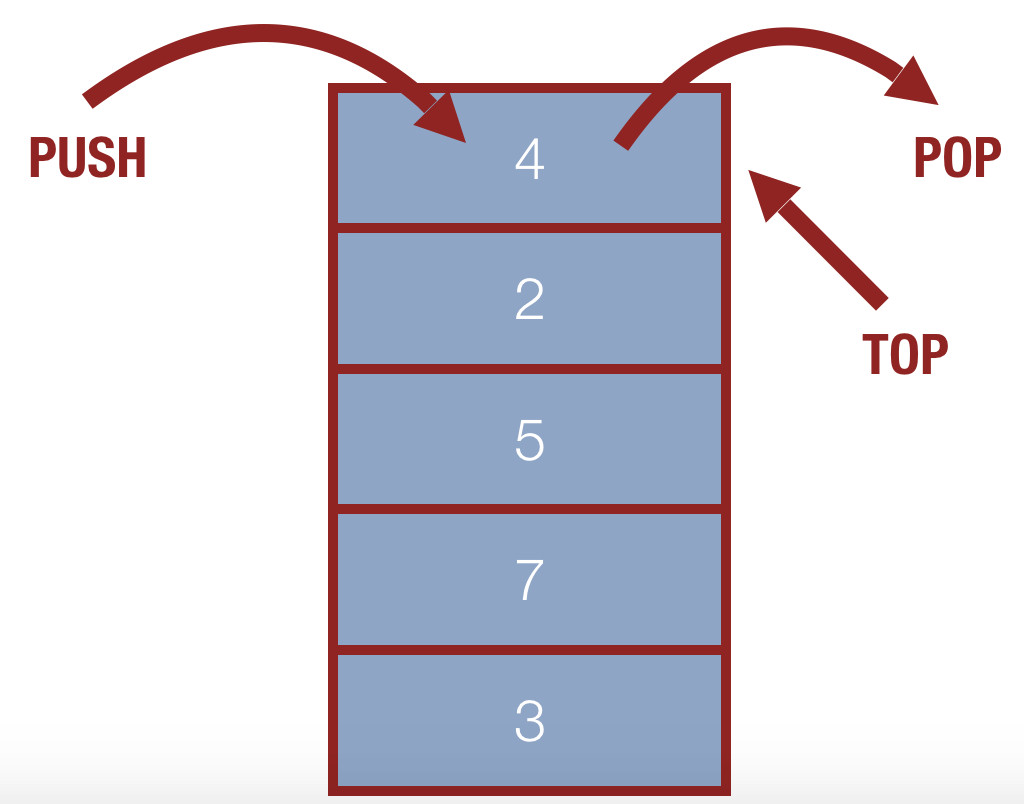
The stack API is different since it is Last in Last out ADT.
We will name the interface as
push(value): place an entity onto the top of the stack.pop(): remove an entity from the top of the stack.top()look at the entity at the top of the stack.isEmpty(): a boolean returning true if the stack is empty.
Postfix expressions
- When you were first learning albebraic expressions, your teacher probably gave you a problem like this and said what is the result?
5 * 4 - 8 / 2 + 9
-
The class got all sorts of differents answers, because no one knew the order of operations yet (the correct answer is 25 by the way). Parenthesis become necessary as well (e.g. 10 / (8 -3)).
-
This is a somewhat annoying problem - it would be nice if there were a better way to do arithmetic so we didn’t have to worry about order of operations and parenthesis.
-
As it turns out, there is a better way! We can use a system of arithmetic called
postfix notation. The expression above would become the following:
5 4 * 8 2 / - 9 +
Given a postfix notation like the one presented above, write a program using stack and queue to evaluate the value of this expression.
